Аннотация. Урок посвящен работе с матрицами — прямоугольными таблицами.
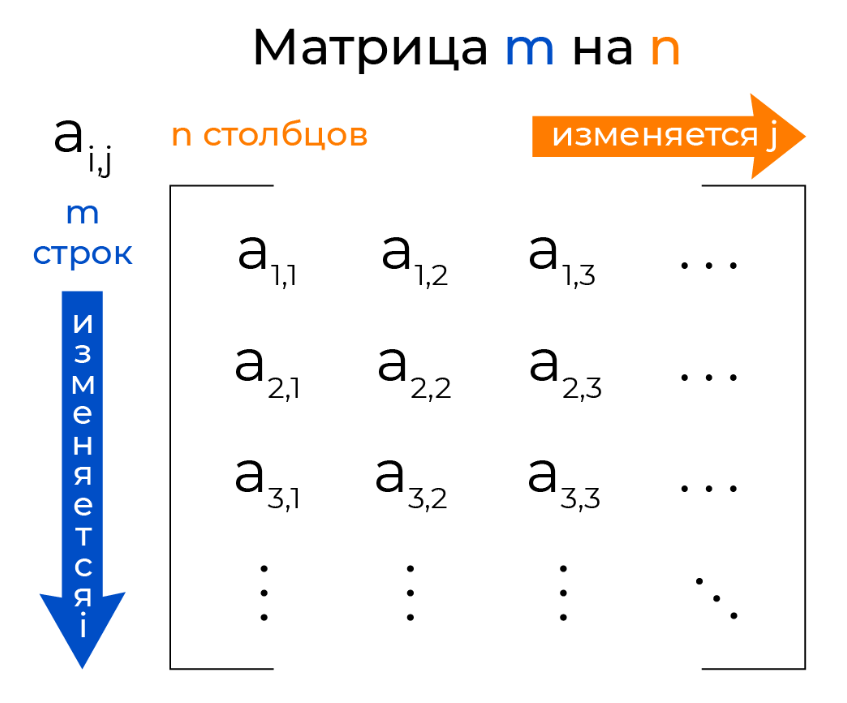
В прошлых уроках мы изучили вложенные списки, то есть списки, входящие в качестве элементов в другие списки. Частный случай вложенных списков — матрицы. Это прямоугольные таблицы, заполненные какими-то значениями, обычно числами.

Матрицы часто применяются в математике, так как многие задачи с их помощью гораздо проще сформулировать, записать и решить.
Для работы с матрицами нужно уметь получать элемент i-й строки j-го столбца. Для этого обычно заводят список строк матрицы, где каждая строка — список элементов. Получается вложенный список или список списков. Теперь, чтобы получить определенный элемент, достаточно из списка строк матрицы выбрать i-ю и взять j-й элемент этой строки.
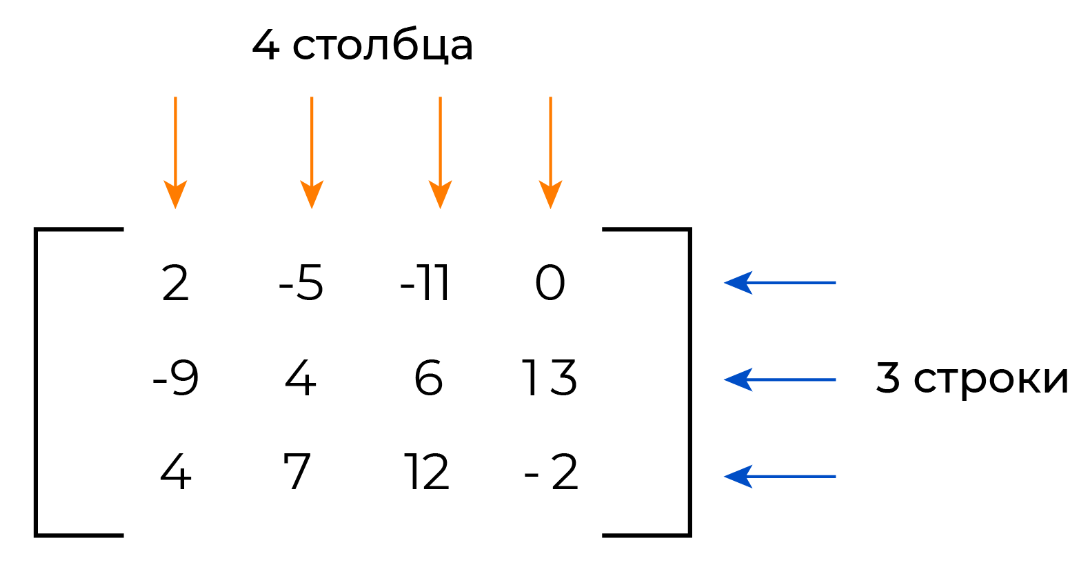
Давайте заведем матрицу размера 3×4(3 строки и 4 столбца), содержащую числа, и получим элемент на позиции (2, 3), то есть элемент второй строки в третьем столбце.
matrix = [[2, -5, -11, 0],
[-9, 4, 6, 13],
[4, 7, 12, -2]]
print(matrix[1][2]) # вывод элемента на позиции (2, 3)
В переменной matrix хранится вся матрица, при этом matrix[1] — список значений во второй строке, matrix[1][2] — элемент в третьем столбце этой строки.
В математике нумерация строк и столбцов начинается с единицы, а не с нуля. По договоренности сначала всегда указывается строка, а затем — столбец. Элемент на i-ой строке, j-м столбце матрицы aa обозначается так – (a_{ij})
Чтобы перебрать элементы матрицы, необходимо использовать вложенные циклы. Например, выведем на экран все элементы матрицы, перебирая их по строкам:
rows, cols = 3, 4 # rows - количество строк, cols - количество столбцов
matrix = [[2, 3, 1, 0],
[9, 4, 6, 8],
[4, 7, 2, 7]]
for r in range(rows):
for c in range(cols):
print(matrix[r][c], end=' ')
print()
Результатом работы такого кода будет:
2 3 1 0
9 4 6 8
4 7 2 7
Для перебора элементов матрицы по столбцам можно использовать следующий код:
rows, cols = 3, 4 # rows - количество строк, cols - количество столбцов
matrix = [[2, 3, 1, 0],
[9, 4, 6, 8],
[4, 7, 2, 7]]
for c in range(cols):
for r in range(rows):
print(matrix[r][c], end=' ')
print()
Результатом работы такого кода будет:
2 9 4
3 4 7
1 6 2
0 8 7
Рассмотрим программный код:
rows, cols = 3, 4 # rows - количество строк, cols - количество столбцов
matrix = [[277, -930, 11, 0],
[9, 43, 6, 87],
[4456, 8, 290, 7]]
for r in range(rows):
for c in range(cols):
print(matrix[r][c], end=' ')
print()
Результатом работы такого кода будет:
277 -930 11 0
9 43 6 87
4456 8 290 7
Выведенная матрица не сильно похожа на упорядоченный прямоугольник. Элементы матрицы имеют разное количество разрядов и результат вывода получается смазанным. Для решения проблемы удобно использовать строковые методы ljust() и rjust().
Строковый метод ljust() выравнивает текст по ширине, добавляя пробелы в конец текста.
Результатом выполнения следующего кода:
print('a'.ljust(3))
print('ab'.ljust(3))
print('abc'.ljust(3))
будет:
a⎵⎵
ab⎵
abc
Исходная строка не обрезается, даже если в ней больше символов, чем нужно.
Результатом выполнения следующего кода:
print('abcdefg'.ljust(3))
будет:
abcdefg
Строковый метод ljust() использует вместо пробела другой символ, если передать ему второй аргумент, необязательный.
Результатом выполнения следующего кода:
print('a'.ljust(5, '*'))
print('ab'.ljust(5, '$'))
print('abc'.ljust(5, '#'))
будет:
a****
ab$$$
abc##
Строковый метод rjust() выравнивает текст по ширине, добавляя пробелы в начало текста.
Результатом выполнения следующего кода:
print('a'.rjust(3))
print('ab'.rjust(3))
print('abc'.rjust(3))
будет:
⎵⎵a
⎵ab
abc
Исходная строка не обрезается, даже если в ней больше символов, чем нужно.
Результатом выполнения следующего кода:
print('abcdefg'.rjust(3))
будет:
abcdefg
Строковый метод rjust() использует вместо пробела другой символ, если передать ему второй аргумент, необязательный.
Результатом выполнения следующего кода:
print('a'.rjust(5, '*'))
print('ab'.rjust(5, '$'))
print('abc'.rjust(5, '#'))
будет:
****a
$$$ab
##abc
Применив метод ljust() для выравнивания столбцов, при выводе таблицы мы получим следующий код:
rows, cols = 3, 4 # rows - количество строк, cols - количество столбцов
matrix = [[277, -930, 11, 0],
[9, 43, 6, 87],
[4456, 8, 290, 7]]
for r in range(rows):
for c in range(cols):
print(str(matrix[r][c]).ljust(6), end='')
print()
Результатом выполнения такого кода будет:
277 -930 11 0
9 43 6 87
4456 8 290 7
Матрица с одинаковым количеством строк и столбцов называется квадратной. У квадратной матрицы есть две диагонали:
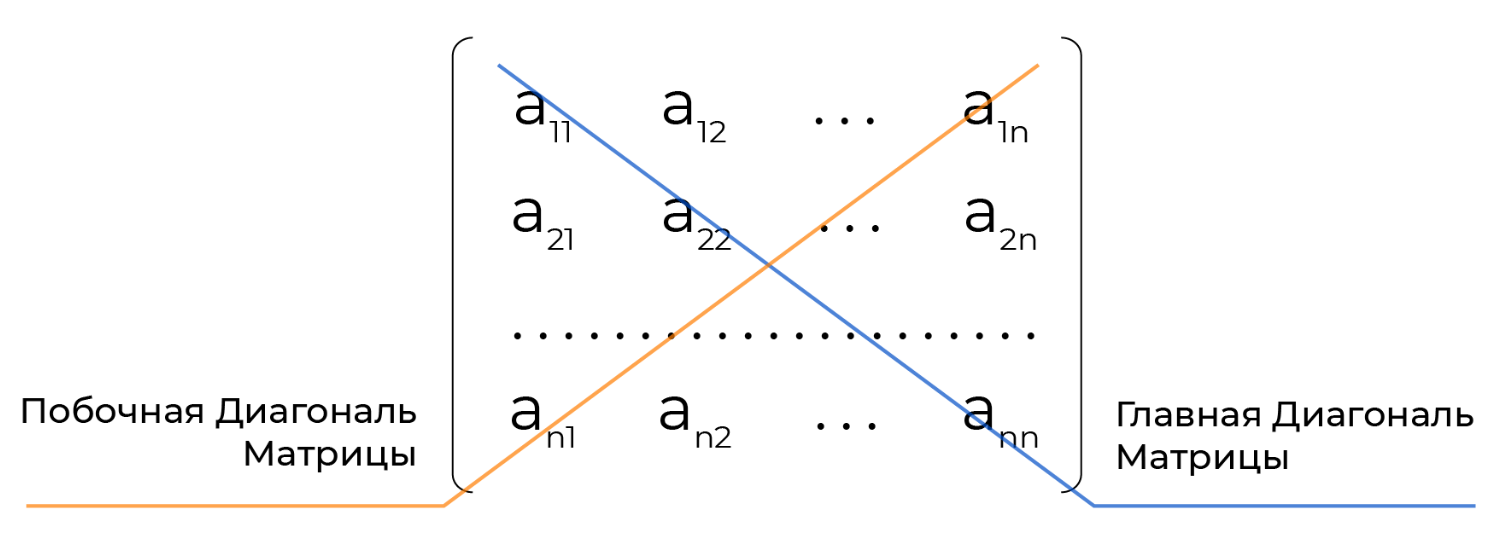
Элементы с равными индексами i == j находятся на главной диагонали. Такие элементы обозначаются matrix[i][i].
Элементы с индексами i и j, связанными соотношением i + j + 1 = n (или j = n - i - 1), где n — размерность матрицы, находятся на побочной диагонали.
Таким образом, чтобы установить элементы главной или побочной диагонали, достаточно одного цикла.
Результатом выполнения следующего кода:
n = 8
matrix = [[0]*n for _ in range(n)] # создаем квадратную матрицу размером 8×8
for i in range(n): # заполняем главную диагональ единицами, а побочную двойками
matrix[i][i] = 1
matrix[i][n-i-1] = 2
for r in range(n): # выводим матрицу
for c in range(n):
print(matrix[r][c], end=' ')
print()
будет:
1 0 0 0 0 0 0 2
0 1 0 0 0 0 2 0
0 0 1 0 0 2 0 0
0 0 0 1 2 0 0 0
0 0 0 2 1 0 0 0
0 0 2 0 0 1 0 0
0 2 0 0 0 0 1 0
2 0 0 0 0 0 0 1
Индексыi и jэлементов на главной диагонали связаны соотношением i = j. Индексы i и jэлементов на побочной диагонали связаны соотношением i + j + 1 = n (или j = n - i - 1), где n — размерность матрицы.
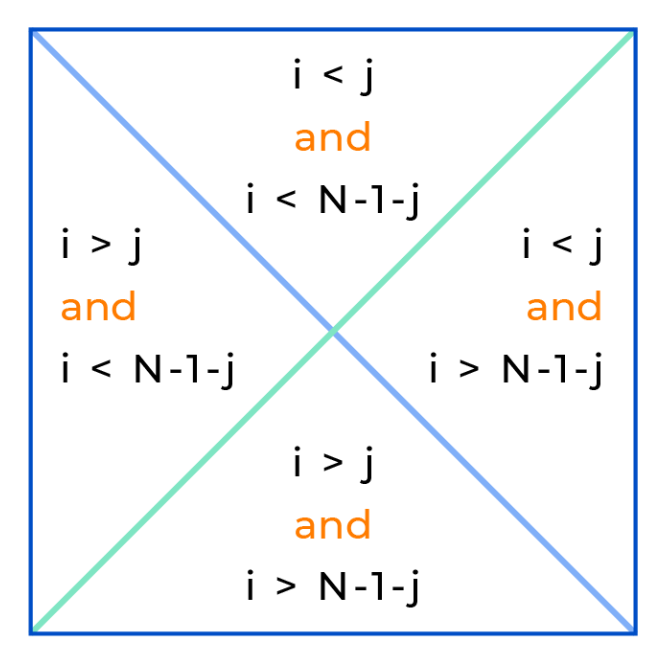
Заметим также, что:
i < j, если ниже - i > j.i + j + 1 < n, если ниже - i + j + 1 > n.Примечание 1. Чтобы понять, в какой области лежит элемент можно воспользоваться следующей картинкой.
Примечание 2. Используйте функцию print_matrix() для вывода квадратной матрицы размерности n:
def print_matrix(matrix, n, width=1):
for r in range(n):
for c in range(n):
print(str(matrix[r][c]).ljust(width), end=' ')
print()
Примечание 3. Для считывания матрицы из n строк, заполненной числами, удобно использовать следующий код:
n = int(input())
matrix = []
for i in range(n):
temp = [int(num) for num in input().split()]
matrix.append(temp)